Simon Lebus asks why we are struggling with providing high-quality maths education and what we need to change to attract the next generation of skilled mathematical minds.
GCSE results day falls on Thursday 24th August this year. We will know then the impact on student attainment levels of this year’s maths GCSE, the first year that the new ‘big fat’ reformed maths GCSE - designed to be more challenging and with more content - has been taken. There are considerable concerns that the greater level of difficulty may end up putting students off progressing on to maths A Level. The Mathematical Association has done research, featured in the TES, that suggests an ‘alarming decline’ in the number of 16 year olds wishing to progress to maths A Level after their experience of being taught and taking the new GCSE. The Department for Education (DfE) has responded by correctly pointing out that the overall trend over time is towards an increased uptake of maths A Level (over the last few decades it has always vied with a couple of other subjects for the position of most popular A Level) but we won't really know until we have firm teaching group sizes and then exam entries some time later. Changed qualifications can produce surprises, such as physics being an unlikely winner from the 2000 reforms of A Level.
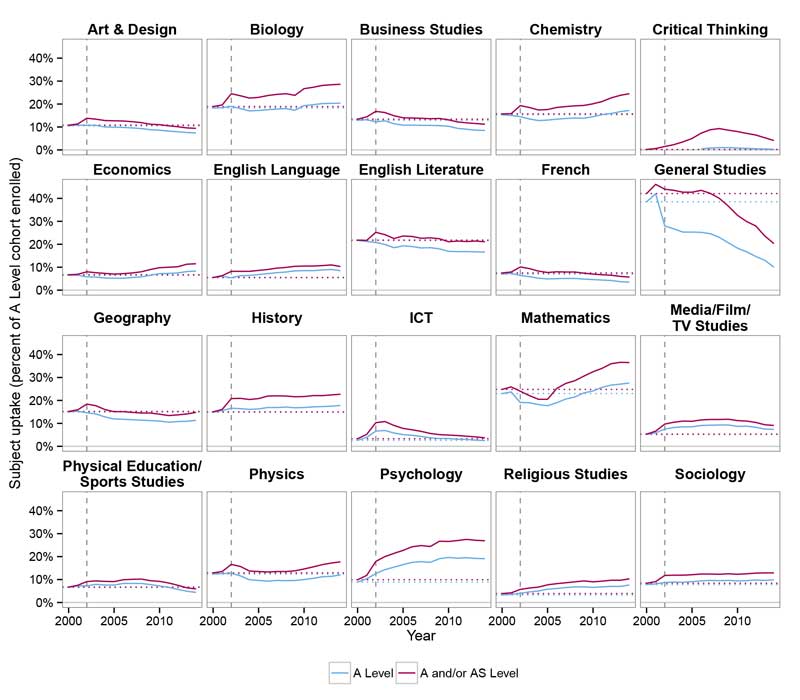
However, a good reason for doubting the DfE’s optimism is the experience of when the new Curriculum 2000 A and AS Level qualifications came in in 2002. The maths paper in 2002 was deemed especially challenging and research by our Data and Analytics team show that entry numbers took some five years to recover to their pre 2002 peak (see graph below). What this demonstrates is, first, that the introduction of reformed qualifications is always a time of maximum risk for the public exam system, as it is technically challenging to carry standards forward from the old to the new system and second, that a failure to get that right can impact student subject choices for several years to come. This all comes at a time when there already exist concerns about shortages of specialist math teachers in the school system and anxieties among employers about the shortage of maths skills among young people entering the work force.
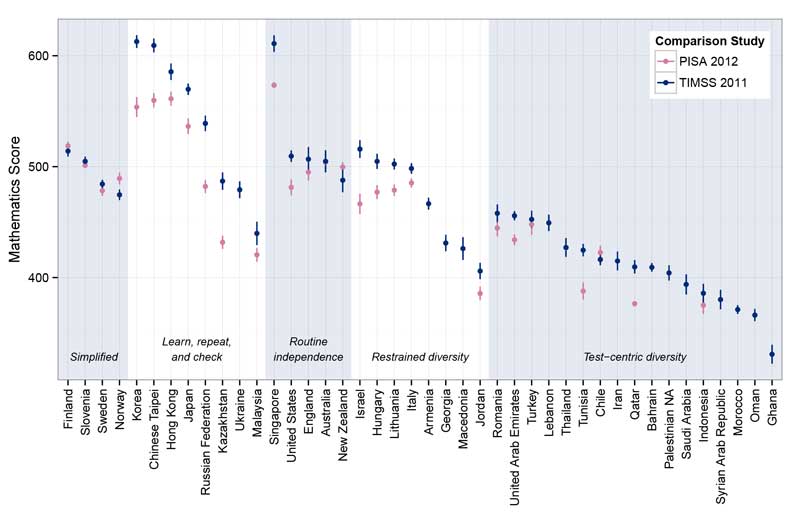
We are not alone in having this problem and many advanced economies struggle with providing high quality maths education, for many of the same reasons, which include shortages of specialist teachers, uncertainty about the best pedagogical approaches, and lack of student confidence. Our own research team has examined different approaches to maths teaching (hyperlink relates to graph below) in countries such as China and Singapore, noted for the numbers of highly proficient maths students that they produce, and has found that an approach focused on the development of an understanding of underlying mathematical concepts accompanied by good levels of procedural fluency, all supported by methodical curriculum design, carefully crafted lessons and, in many cases, prescribed and highly structured learning resources is capable of producing consistently good levels of attainment, especially when also supported by heavy investment in teacher professional development.
Another challenge in terms of securing good levels of mathematical competence is to do with successfully identifying those mathematical skills needed for general living, for the pursuit of particular interests, or for specialist purposes, such as the desire to follow a particular career or choose a particular subject for specialist or higher study. Many social science subjects, for example, now require fluency in statistics, whereas natural scientists or engineers would need additional skills in areas such as mechanics. Partly to address this we several years ago set up a project to develop the Cambridge Mathematics framework. The idea was to follow the lead of applied linguists who had developed the Common European Framework of Reference (CEFR) for language learners. This ranks language speakers’ proficiency from A1 (the lowest) to C2 (the highest) in the four separate domains of reading, writing, speaking, and listening. This is a challenging task as maths covers a much less easily defined set of skills, but the concept of trying to create a much more granular map that charts the landscape of mathematical expertise is one that ought to allow educationalists, employers, and other stakeholders to identify particular mathematical competencies needed to succeed in different jobs, professions, or education courses with a much greater degree of precision. That in turn might allow a more bespoke approach to maths education, and perhaps a greater degree of differentiation in exams offered at age 16, thereby avoiding young people falling over the cliff-edge of GCSE, and encouraging more of them to continue with maths into upper secondary and beyond.
Simon Lebus
Group Chief Executive, Cambridge Assessment