December 2020
Summary
In the context of examinations, the phrase "maintaining standards" usually refers to any activity designed to ensure that it is no easier (or harder) to achieve a given grade in one year than in another.
Benton et al (2020) describes a method to inform grade boundaries called simplified pairs that allows us to map scores between test versions using comparative judgement. The aim of this study was to evaluate the accuracy of the simplified pairs method when applied to a mathematics assessment.
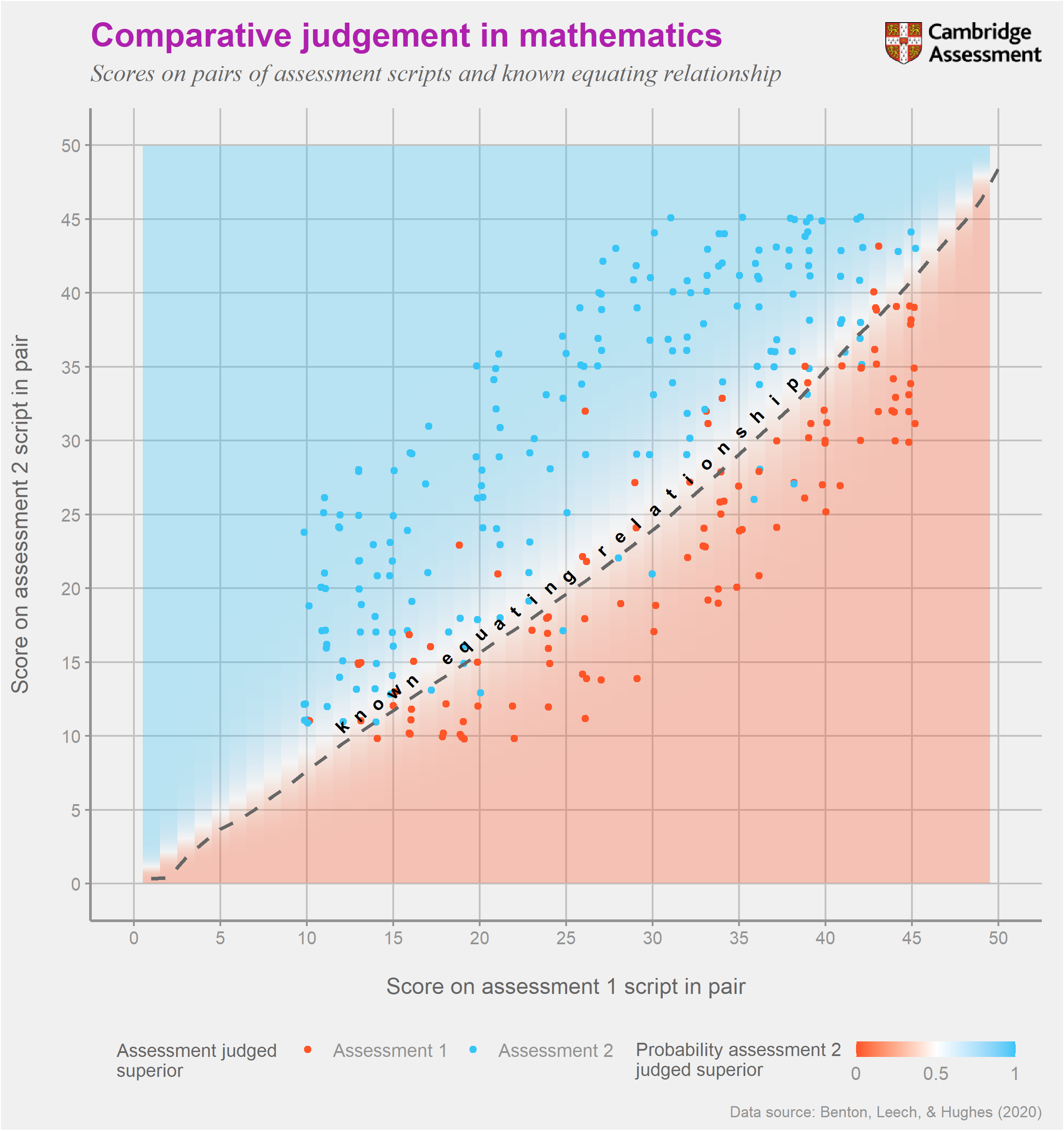
What does the chart show?
The chart shows the results of an experiment to explore whether comparative judgement could accurately identify where grade boundaries should be positioned in maths exams.
The experiment required expert judges (GCSE examiners) to compare pairs of scripts from two different maths assessments. The location of the points in the chart denotes the marks awarded to the scripts from each version within each pair. For example, one comparison was of a script from version 1 awarded 45 out of 50 to a script from version 2 awarded 30 out of 50. For each pair (each point in the chart) judges had to indicate which script represented a better performance in mathematics. The colours of the points indicate the judges’ decisions. Red means they thought the version 1 script was superior, and blue means they thought the version 2 script was superior.
The shading of the chart summarises these judgements by showing how the probability of a judge choosing each version varies depending upon the marks that each were awarded. The white zone is of particular interest as this is where judges are equally likely to select either version as being superior. In other words, it’s the zone where scores on the different versions display equally good performances. This is useful as it helps us identify equivalent scores on different test versions using expert judgement. For example, according to judges, a score of 25 on version 1 is an equivalent performance to a score of 21 on version 2.
For the assessments in this particular experiment we already had accurate estimates of the equivalent score on version 2 for each score on version 1. This was estimated independently using statistical equating and is denoted by the thick dashed line. The fact that this line is on the edge of the white area in the chart indicates that the decisions from judges were broadly consistent with the known relative difficulties of the two tests.
Why is the chart interesting?
At present, we do not have a single definitive source of information about the relative difficulty of assessments over time. This means that we have to rely on methods such as comparable outcomes to set grade boundaries that (largely) hold grade distributions constant over time. Our experimental data suggests that expert judgement, captured using comparative judgement, might provide a fairly accurate addition to such sources of evidence. This may mean that in future we could identify genuine changes in performance over time and ensure that they are reflected in national results.
Further information
Further details can be found in:
Benton, T., Leech, T. & Hughes, S. (2020). Does comparative judgement of scripts provide an effective means of maintaining standards in mathematics?. Cambridge Assessment Research Report. Cambridge, UK: Cambridge Assessment.
Benton, T., Cunningham, E., Hughes, S., and Leech, T. (2020). Comparing the simplified pairs method of standard maintaining to statistical equating. Cambridge Assessment Research Report. Cambridge, UK: Cambridge Assessment.